Inhaltsverzeichnis
- 1 Standardabweichung «einfach erklärt»
- 2 Definition: Standardabweichung
- 3 Die Standardabweichung verständlich berechnet
- 4 Formeln für die Standardabweichung
- 5 Standardabweichung mit Beispiel berechnen
- 6 Ergebnisse zusammenfassen
- 7 Standardabweichung mit „SPSS“ berechnen
- 8 Standardabweichung mit „Excel“ oder „Google Tabellen“ berechnen
- 9 Fazit zur Standardabweichung
- 10 Häufig gestellte Fragen

Statistik ist ausgesprochen komplex – und doch ist es sinnvoll, die Zusammenhänge zu verstehen. Schließlich wirst du nicht nur im Studium mit diesem Thema konfrontiert, sondern in jedem Bereich deines Lebens. Umso wichtiger ist es, die relevanten Begriffe zu kennen und richtig einordnen zu können. In diesem Beitrag erhältst du Informationen zur Bedeutung der Standardabweichung und ihrer konkreten Berechnung.
Definition: Standardabweichung
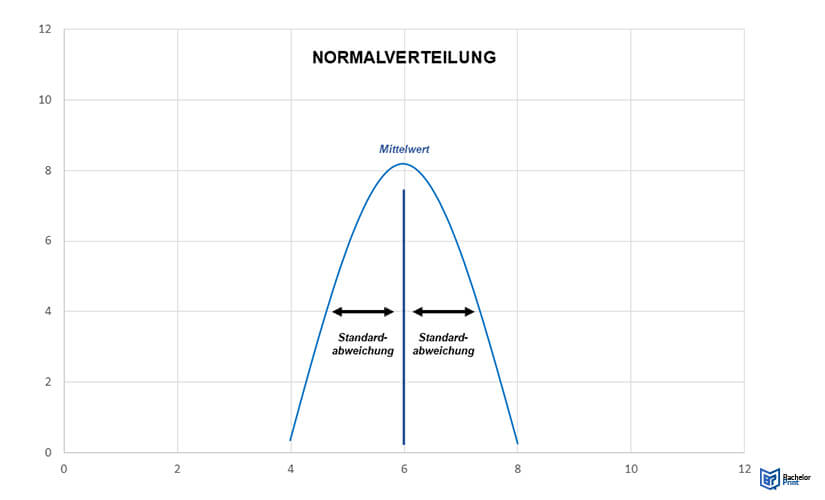
Dieses Streuungsmaß misst die Streubreite der für ein Merkmal in einer Stichprobe erfassten Werte rund um das arithmetische Mittel dieser Werte. Es geht also darum, wie weit alle erfassten Ausprägungen des Merkmals vom Durchschnitt entfernt sind. Bei einer großen Standardabweichung liegen die in der Stichprobe erfassten Werte weit vom Mittelwert entfernt – und umgekehrt. Daraus lassen sich insofern Rückschlüsse ziehen, ob sich die Werte stark voneinander unterscheiden oder nicht.
Für die Normalverteilung gilt folgende pauschale Regel:
- rund 68 % aller gemessenen Werte liegen innerhalb einer Standardabweichung vom Mittelwert – und zwar nach oben und nach unten
- rund 95 % aller Werte liegen innerhalb des Radius von zwei Standardabweichungen
- alle darüberhinausgehenden Werte werden als «Ausreißer» bewertet
Nicht zu verwechseln, aber direkt zusammenhängend: die Varianz als ein weiteres Streuungsmaß, aus dessen Quadratwurzel sich die Standardabweichung ergibt. Die Varianz misst die Verteilung der ermittelten Werte um den Mittelwert. Allerdings lassen sich die Ergebnisse dieser Berechnung schwerer interpretieren.¹
Die Standardabweichung verständlich berechnet
Ein Beispiel soll die Berechnung veranschaulichen:
Liegt das Ergebnis im aufgeführten Beispiel bei 300 Euro, zeigt das klar auf, dass die jeweiligen Mitarbeiter ein ähnliches Gehalt beziehen – und wahrscheinlich einer Gehaltsgruppe angehören. Erhältst du ein deutlich höheres Ergebnis, dürften sie sehr unterschiedlich bezahlt werden.
Formeln für die Standardabweichung
Grundsätzlich gibt es zwei Formeln, die sich in erster Linie auf die Varianz beziehen – nämlich die Stichprobenvarianz und die empirische Varianz. Aus diesen unterschiedlichen Ansätzen lässt sich durch das Ziehen der Quadratwurzel einerseits die Standardabweichung der Grundgesamtheit (Stichprobenvarianz) und andererseits deiner Stichprobe (empirische Varianz) ableiten.³
Standardabweichung mit Beispiel berechnen
Ergebnisse zusammenfassen
Um auf das Notenbeispiel zurückzukommen: Das Ergebnis 1,44 zeigt an, wie weit die erzielten Noten gestreut sind, also von der Durchschnittsnote 3 entfernt liegen – nämlich + oder -1,44.
Je niedriger die Varianz ausfällt, desto enger liegen die in einem Datensatz erfassten Werte beisammen.
Je höher die Varianz, desto weiter liegen sie entfernt.
Es mag auf den ersten Blick wenig Anwendungsgebiete für diese Maßeinheiten der Streuung geben, jedoch sind diese Berechnungen durchaus relevant, wie zum Beispiel im Aktienhandel: Willst du beispielsweise Geld investieren und analysierst deswegen die Kursentwicklung einzelner Aktien, kannst du daraus interessante Rückschlüsse ziehen: Berechne zum Beispiel die durchschnittliche Veränderung des Aktienpreises pro Jahr – und die für die vergangenen zehn Jahre, um dann die Varianz zu ermitteln. Je höher diese ausfällt, umso volatiler ist das entsprechende Wertpapier, also umso größer sind die zu erwartenden Kursschwankungen – und damit auch deine Risiken.
Standardabweichung mit „SPSS“ berechnen
Sehr viel einfacher funktioniert die Berechnung mit „SPSS“, also einer speziellen Statistik- und Analyse-Software von „IBM“. Du gehst folgendermaßen vor:
- «Menü Analysieren» auswählen
- «Deskriptive Statistiken» anklicken
- «Häufigkeiten» anklicken
- Variable auswählen, für die die Berechnung durchgeführt werden soll
- «Statistik» anklicken
- «Streuung» anklicken
- Varianz oder Standardabweichung auswählen²
Standardabweichung mit „Excel“ oder „Google Tabellen“ berechnen
Auch dieses Tool kann dir bei der Berechnung helfen – „Excel“ bietet die Auswahl zwischen zwei Formeln, sodass du diese hier nicht erst von Hand eingeben musst.
So gehst du vor:
- Tabelle für die Werte anlegen
- Werte in die Spalten eintragen – hier A2 bis E2
- Mittelwert berechnen mit „=MITTELWERT(A2:E2)“
- Berechnung durchführen: „=STABW.N(A2:F2)“ für Standardabweichung bzw. „=VAR.S(A2:F2)“ für Varianz
Fazit zur Standardabweichung
Wie weit die Werte einer Stichprobe vom Mittelwert abweichen, mag zunächst nicht interessant erscheinen. Allerdings gibt es durchaus einige Gründe, die Standardabweichung zu berechnen. Dazu kannst du nicht nur die kompliziert wirkenden Formeln nutzen, sondern auf Berechnungstools zurückgreifen.
Häufig gestellte Fragen
Hierbei handelt es sich um ein bedeutendes Streuungsmaß in der Statistik: Die über verschiedene Wege zu berechnende Standardabweichung beschreibt die durchschnittliche Abweichung der Ergebnisse vom Mittelwert.
Mit „xi“ ist der Beobachtungswert gemeint. Dabei handelt es sich genau genommen um die erfassten Daten eines Merkmals, die du für die Berechnung einer Standardabweichung vom Mittelwert benötigst.
Der Mittelwert eines Merkmals lässt sich durch die Summe aller erfassten Werte und die anschließende Division durch die Anzahl der Werte ermitteln. Du erhältst also den durchschnittlichen Wert.
Auch bei der Varianz handelt es sich um ein Streuungsmaß. Allerdings beschreibt dies die Verteilung der Messergebnisse um den Mittelwert.
Zur Berechnung beider Streuungsmaße kannst du Tools wie „Excel“ einsetzen. Hier reicht es aus, die Daten und die jeweilige Formel einzugeben, um ein Ergebnis zu erhalten. Alternativ gibt es beispielsweise die spezielle Statistik-Software „SPSS“.