
Das Chi-Quadrat und der Chi-Quadrat-Tests kommt in der Statistik und somit auch in der Marktforschung und der Psychologie regelmäßig zum Einsatz.
Kategorische Variablen gehören eindeutigen Kategorien, wie beispielsweise Geschlecht oder Religionszugehörigkeit, an. Man unterscheidet zwischen nominalen und ordinalen Variablen.
Erstere bezeichnen Kategorien, die sich nicht in eine natürliche Reihenfolge einordnen lassen. Letztere hingegen beschreiben Kategorien, die eine natürliche Reihenfolge aufweisen. Der Chi-Quadrat-Test wird auch als Kontingenzanalyse bezeichnet. Er beantwortet die Frage, ob ein Zusammenhang zwischen zwei kategorialen Variablen besteht und wie stark dieser Zusammenhang ist.¹
Definition: Chi-Quadrat
Anhand des Chi-Quadrat-Tests erkennt man, ob ein Zusammenhang zwischen zwei nominal- oder ordinalskalierten Variablen besteht. In einer Kontingenzanalyse wird untersucht, ob die in einer Stichprobe vorkommenden Häufigkeiten in bedeutendem Maße von jenen Häufigkeiten abweichen, die man bei der jeweiligen Problemstellung erwarten würde.
Die beobachteten Häufigkeiten werden mit den erwarteten Häufigkeiten verglichen. Dadurch werden Abweichungen untersucht. Beim Chi-Quadrat handelt es sich um ein nicht standardisiertes Zusammenhangsmaß. Dies bedeutet, dass nur eine begrenzte Interpretation der erhaltenen Werte möglich ist.
Chi-Quadrat: Formel
Das Chi-Quadrat wird anhand der folgenden Formel berechnet:
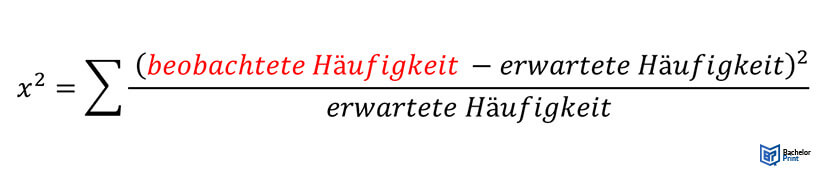
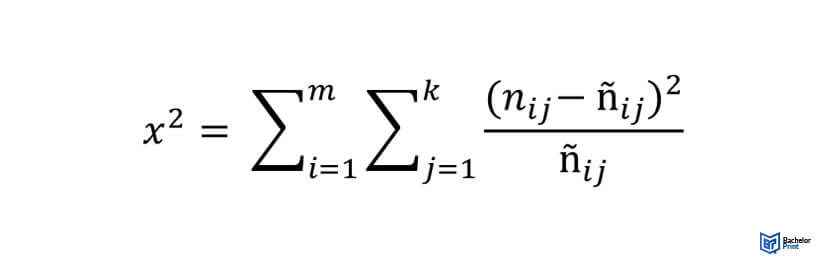
x² = Chi-Quadrat
m = Gesamtanzahl der Zeilen
k = Gesamtanzahl der Spalten
nij = absolute Häufigkeit der Kombination aus i-Zeile und j-Spalte (beobachtete Häufigkeit)
ñij = erwartete Häufigkeit der Kombination aus i-Zeile und j-Spalte (erwartete Häufigkeit)
Mit dem Chi-Quadrat den Kontingenzkoeffizienten berechnen
Der Chi-Quadrat-Koeffizient ist ein nicht standardisiertes Zusammenhangsmaß und als solches nur begrenzt vergleichbar. Konkrete Schlüsse lassen sich aus diesem Wert also nicht ziehen. Genauer gesagt ist kein Zusammenhang zwischen Geschlecht und der präferierten Zeitung zu erkennen.
Möchte man nun genauere Zusammenhänge finden, muss man den Chi-Quadrat-Koeffizienten in den Kontingenzkoeffizienten nach Pearson oder in Cramers V umwandeln. Den Kontingenzkoeffizienten erhält man mithilfe der entsprechenden Formel. Der Kontingenzkoeffizient kann Werte wischen 0 und 1 annehmen, wobei 0 für keinen und 1 für einen völligen Zusammenhang zwischen den Merkmalen steht.²
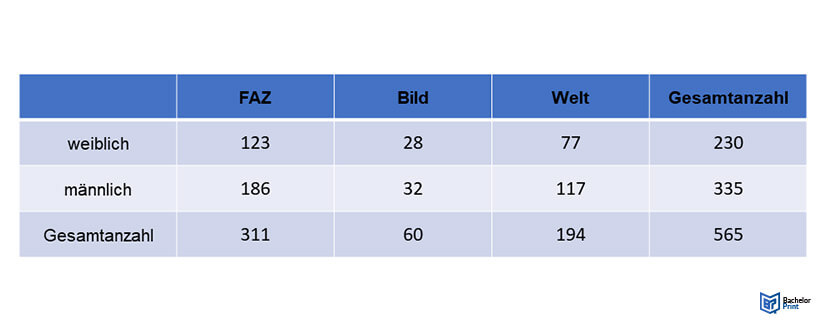
Von einer Kreuztabelle ablesen
Eine Kreuztabelle stellt das Verhältnis zwischen zwei kategorialen Variablen her. In unserem Beispiel sind es das Geschlecht und die präferierte Zeitung. Man kann also mithilfe der Kreuztabelle erfahren, wie häufig die Kombination der Ausprägungen zweier Merkmale auftritt.
Aus der Kreuztabelle lassen sich absolute und relative Häufigkeiten ablesen. Als absolute Häufigkeiten wird der Wert bezeichnet, der angibt, wie oft die Kombination aus zwei Merkmalen vorkommt. Die relative Häufigkeit hingegen gibt an, wie oft eine bestimmte Kombination in Bezug zu allen Fällen vorkommt. Sie wird in der Regel in Prozent angegeben.³
Häufig gestellte Fragen
Das Chi-Quadrat gibt an, ob ein Zusammenhang zwischen zwei Variablen besteht. Kategorische Variablen können einen eindeutigen Wert bzw. eine eindeutige Kategorie haben.
Nein, der Chi-Quadrat-Wert ist nicht standardisiert und somit nur begrenzt vergleichbar. Der Chi-Quadrat-Wert lässt sich jedoch in den Kontingenzkoeffizienten nach Pearson oder in Cramers V umrechnen – beides sind standardisierte Koeffizienten.
Kreuztabellen werden auch als Kontingenztafeln bezeichnet und geben einen Überblick über zwei Variablen. Die Kreuztabelle gibt Auskunft über die Häufigkeit einer bestimmten Kombination zweier Merkmale.
Das Chi-Quadrat kommt überall dort zum Einsatz, wo statistische Werte erfasst werden müssen, also beispielsweise in der Statistik, der Psychologie oder der Marktforschung.
Um das Chi-Quadrat berechnen zu können, muss man die entsprechende Formel kennen. Dann setzt man die jeweiligen Werte ein und erhält das gewünschte Ergebnis.
Quellen
¹ Hochschule Luzern: Pearson-Chi-Quadrat-Test (Kontingenzanalyse), in: Empirical Methods, Ressourcen für empirische Methoden, o.D., [online] https://www.empirical-methods.hslu.ch/entscheidbaum/zusammenhaenge/pearson-chi-quadrat/ (10.01.2023)
² Humboldt-Universität zu Berlin: Kontingenz, in: Bivariate Statistik, 2020, [online] https://wikis.hu-berlin.de/mmstat/Kontingenz (10.01.2023)
³ Universität Flensburg: Kreuztabellen und Häufigkeitstabellen, in: Methodenlehre, o.D., [online] https://www.uni-flensburg.de/fileadmin/content/abteilungen/methodenlehre/dokumente/downloads/iris-albertin/kreuztabellen-haeufigkeitstabellen.pdf (abgerufen am 10.01.2023)
