Wer für eine Abschlussarbeit eine Studie durchgeführt hat, sitzt am Ende häufig auf einer Vielzahl empirischer Daten, die ausgewertet werden müssen. Dazu kannst du Kennzahlen aus der deskriptiven Statistik verwenden. Neben den Streuungsparametern sind vor allem die Lageparameter von Bedeutung. Die wichtigsten Kennzahlen der Lageparameter und alles, was du dazu wissen musst, zeigen wir dir in diesem Beitrag.
Inhaltsverzeichnis
Lageparameter «einfach erklärt»
Lageparameter beschreiben den Mittelpunkt einer Datensammlung. Das bekannteste Lageparameter ist das arithmetische Mittel, das auch als Durchschnittswert bekannt ist. Neben dem arithmetischen Mittel sind der Modus und der Median die wichtigsten Lageparameter.
Definition: Lageparameter
In der deskriptiven Statistik nutzt man Lageparameter, um den Mittelpunkt einer Verteilung von Daten näher zu beschreiben. Umgangssprachlich werden die Lageparameter auch als Durchschnittswerte bezeichnet, in der Fachsprache ist auch der Begriff Lagemass geläufig. Die wichtigsten Lageparameter sind:
- das arithmetische Mittel,
- der Median und
- der Modus.
Diese Werte nähern sich dem Zentralwert eines Datensatzes auf unterschiedliche Arten an.1
Lageparameter im Überblick
Im Folgenden kannst du dir einen Überblick über die wichtigsten Charakteristika der drei Lageparameter verschaffen.
Arithmetisches Mittel
Das arithmetische Mittel wird auch als Mittelwert oder Durchschnittswert bezeichnet. Es handelt sich um das bekannteste Lageparameter, das den statistischen Durchschnitt aller Werte eines Datensatzes angibt. Dafür werden alle Werte addiert, ihre Summe wird durch die Anzahl der Werte geteilt.2
Ein Nachteil des arithmetischen Mittels zeigt sich in seiner hohen Anfälligkeit gegenüber Ausreissern. Befindet sich in einem Datensatz ein extrem hoher oder niedriger Wert, wird dieser den Mittelwert stark in eine Richtung reissen. Dadurch kann es passieren, dass ein falsches Bild von der Allgemeinheit des Datensatzes entsteht.
Zudem ist dieser Lageparameter nur auf metrischen Skalen messbar. Metrische Daten sind solche, die du in eine Rangreihenfolge bringen und anschliessend hinsichtlich ihrer Abstände beurteilen kannst. Dazu zählen beispielsweise:
- Körpergrössen,
- das Alter,
- das Einkommen oder
- Temperaturen.
Hier können die Daten sortiert werden, beispielsweise von der jüngsten zur ältesten Person, und es lässt sich die Aussage treffen, dass eine Person doppelt so alt wie die andere ist.
Median
Als Median bezeichnet man den Wert, der in der exakten Mitte einer Datenverteilung liegt. Er wird auch Zentralwert genannt. Eine Hälfte der Daten ist immer kleiner als der Median, die andere grösser. Dadurch stellt dieses Lageparamter auch bei asymmetrischen Verteilungen und Ausreissern ein stabiles Mass dar.
Ist die Anzahl der Werte ungerade, kann einer der Datenpunkte als Median genutzt werden. Bei geraden Anzahlen wird auf die beiden mittleren Werte zurückgegriffen, deren Durchschnitt dann als Median fungiert. So werden beispielsweise fünf Messwerte nach ihrer Grösse geordnet. Der dritte Wert ist dann der Median. Sind es sechs Messwerte, ist der Median der Durchschnitt des dritten und des vierten Wertes.3
Neben metrischen Skalen kann dieses Lageparameter auch aus ordinalskalierten Daten berechnet werden. Dabei handelt es sich um Werte, die du zwar in eine Reihenfolge bringen kannst, doch du kannst keine Aussagen über Abstände und Verhältnisse treffen. Beispielsweise kannst du Schulnoten danach ordnen, wie gut sie sind. Du kannst jedoch nicht sagen, die Note 2 sei doppelt so gut wie die Note 4.
Modus
Der Modus ist der Messwert, der in einem Datensatz am häufigsten vorkommt. Er ist also eine Art typischer Wert für die Erhebung.
Neben metrischen und ordinalskalierten Daten ist der Modus als einziges Lageparameter auch auf nominale Daten anwendbar. Das sind Daten, die nicht in eine Rangreihenfolge gebracht werden können. Du kannst also nur sagen, ob es einen Unterschied zwischen den Werten gibt, aber nicht, welcher besser oder schlechter ist. Nominale Daten sind beispielsweise:
- Farben
- Postleitzahlen
- Vornamen
Lageparameter am Beispiel erklärt
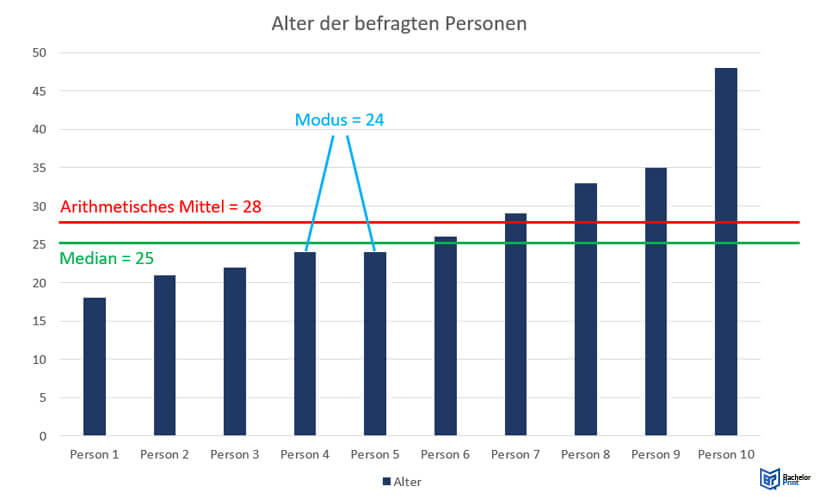
Die Lageparameter sollen nun am Beispiel einer statistischen Erhebung zum Alter von zehn Personen erklärt werden. Die Daten des Alters in Jahren sehen folgendermassen aus:
| 18 | 21 | 22 | 24 | 24 | 26 | 29 | 33 | 35 | 48 |
Arithmetisches Mittel
Das arithmetische Mittel stellt den Durchschnittswert aller Datenpunkte dar. In unserem Beispiel wird dieses Lageparameter berechnet, indem wir alle erfassten Körpergrössen addieren und dann durch ihre Anzahl teilen:
Ergebnis: Das arithmetische Mittel des Datensatzes beträgt 28. Im Durchschnitt sind die Personen 28 Jahre alt.
Problem des arithmetischen Mittels
Was auf das Alter von Personen zutrifft, kann bei anderen Datensätzen ein falsches Bild erschaffen. Zum Beispiel:
Eine Gruppe aus fünf Teenagern wird befragt, wie oft sie schon die Schule geschwänzt haben. Vier von ihnen haben noch nie geschwänzt, der Fünfte hat bereits zehn Mal die Schule geschwänzt. Also:
Es sieht nun aus, als hätte jeder der anwesenden Teenager zwei Mal die Schule geschwänzt, obwohl sich der Grossteil von ihnen gar nichts haben zuschulden kommen lassen.
Merke: Das arithmetische Mittel als Lageparameter einer Statistik kann eine gute Orientierung bieten, muss aber stets kritisch betrachtet werden.1
Median
Der Median ist der Wert, der genau in der Mitte einer sortierten Reihe aus Messwerten liegt. Er teilt diese in eine kleinere und eine grössere Hälfte. Wir betrachten unseren Datensatz mit dem Alter der 10 Personen:
| 18 | 21 | 22 | 24 | 24 | 26 | 29 | 33 | 35 | 48 |
Genau in der Mitte liegen die beiden Zahlen 24 und 26. Um den Median erhalten, müssen wir den Durchschnitt dieser Zahlen errechnen.
Ergebnis: Der Median ist 25, denn es handelt sich um die Mitte von 24 und 26 Jahren. Die eine Hälfte der Daten (18; 21; 22; 24; 24) ist kleiner als der Median von 25 Jahren, die andere Hälfte der Daten (26; 29; 33; 35; 48) ist grösser.
Modus
Der Modus ist der Wert, der in einem Satz aus Beobachtungsdaten am häufigsten auftritt. Gibt es zwei solche Werte, stellt sich zunächst die Frage, ob sie direkt nebeneinander liegen oder nicht. Im Falle einer Nachbarschaft kannst du den Durchschnitt aus beiden Werten bilden und diesen als Modus angeben. Liegen die Datenpunkte nicht nebeneinander, sollten sie beide als Modus angegeben werden.
| Alter | 18 | 21 | 22 | 24 | 26 | 29 | 33 | 35 | 48 |
| Häufigkeit | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
Alle Angaben treten einmal auf, mit Ausnahme der 24, die zweimal vorkommt.
Ergebnis: Der Modus des Datensatzes ist 24. Denn das Alter 24 kommt in der Erhebung am häufigsten vor.
Häufig gestellte Fragen
Lageparameter sind Kennzahlen, die die zentrale Lage beziehungsweise den Mittelpunkt einer Datenverteilung beschreiben. Die wichtigsten Lageparameter sind das arithmetische Mittel, der Median und der Modus.
Das arithmetische Mittel ist ein statistischer Mittelwert aller Beobachtungsdaten in einer Erhebung. Umgangssprachlich ist dieses Lageparameter als klassischer Durchschnitt bekannt.
Der Median ist der Datenpunkt, der genau in der Mitte einer Reihe aus Messwerten liegt. Diese muss zur Bestimmung des Medians nach der Grösse geordnet werden.
Als Modus wird der Wert bezeichnet, der in einer Datenreihe am häufigsten auftritt. Es handelt sich bei diesem Lageparameter also um den Wert, zu dem der Datensatz tendiert.
Lageparameter sind Zahlen, die den Mittelpunkt einer Datenverteilung definieren und beschreiben. Die Streuungsparameter hingegen beschreiben den Verlauf der Daten auf beiden Seiten des Mittelpunktes.1
Quellen
1 Statista: Definition Lageparameter, in: de.statista.com, o. D., [online] https://de.statista.com/statistik/lexikon/definition/80/Lageparameter/ (zuletzt abgerufen am 04.01.2023)
2 Statista: Definition Mittelwert und arithmetisches Mittel, in: de.statista.com, o. D., [online] https://de.statista.com/statistik/lexikon/definition/91/mittelwert_und_arithmetisches_mittel/ (zuletzt abgerufen am 04.01.2023)
3 Statista: Definition Median, in: de.statista.com, o. D., [online] https://de.statista.com/statistik/lexikon/definition/85/median/ (zuletzt abgerufen am 04.01.2023)