Inhaltsverzeichnis

Im Bereich der Statistik gibt es zahlreiche Fachbegriffe, die Studierende kennen müssen. Manche davon sind leichter zu verstehen als andere. Zu einen dieser Begriffe gehört der „Standardfehler“. Alles was du dazu wissen musst und wozu du den Standardfehler brauchst, erklären wir dir in diesem Beitrag.
Definition: Standardfehler
Der Standardfehler wird auch als Stichprobenfehler oder «standard error of the mean (SEM)» bezeichnet. Er gibt an, wie stark der Mittelwert einer Stichprobe vom Mittelwert der Grundgesamtheit abweicht.
Wenn du aus derselben Grundgesamtheit verschiedene Stichproben ziehst, um den jeweiligen Mittelwert zu berechnen, wirst du es mit verschiedenen Mittelwerten zu tun haben. Die Streuung dieser Mittelwerte wird als Standardabweichung bezeichnet. Der Standardfehler hingegen gibt die Standardabweichung sämtlicher Stichproben an, die aus der Grundgesamtheit gezogen werden können. Wenn dir die Standardabweichung des Mittelwerts unbekannt ist, kannst du den Standardfehler nur schätzen.
Als Standardfehler bezeichnet man somit das Streuungsmaß einer Schätzfunktion für einen unbekannten Parameter der Grundgesamtheit. Je kleiner der Standardfehler ist, desto genauer lässt sich der unbekannte Parameter bestimmen. Der Stichprobenfehler ist vom Umfang der Stichprobe und der Varianz der Grundgesamtheit abhängig. Ein großer Stichprobenumfang und eine geringere Varianz führen zu einem kleineren Fehler. Bei kleinen Stichproben wird der Fehler in der Regel unterschätzt. Bei einer Stichprobe mit zwei Personen beträgt die Unterschätzung 25 %, bei sechs Personen sind es nur noch 5 %.
Anwendung und Berechnung vom Standardfehler
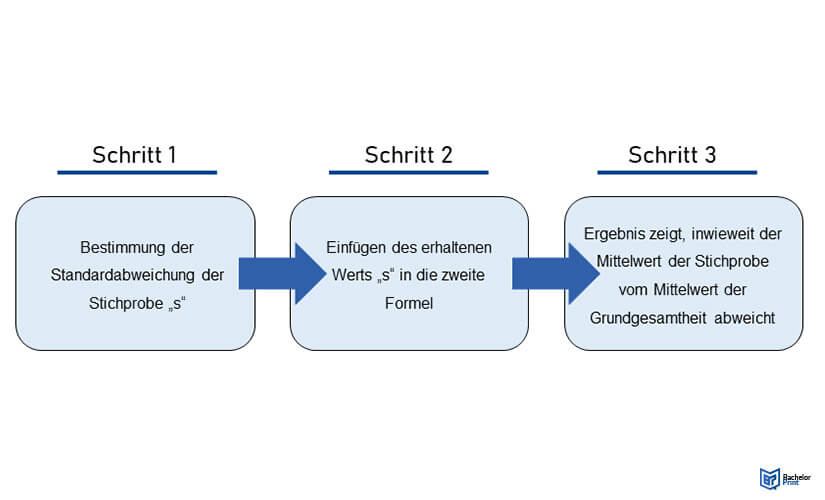
Zur Berechnung des Standardfehlers stehen dir zwei verschiedene mathematische Formeln zur Verfügung. Du musst die dir bekannten Werte in die jeweilige Formel einfügen, um das gewünschte Ergebnis zu erhalten. Welche Formel du verwendest, hängt davon ab, ob dir der Mittelwert und die Standardabweichung der Grundgesamtheit bekannt sind. Ist dies nicht der Fall, kommt es zu einer Schätzung des Fehlers. In den meisten Fällen wird die zweite Formel benutzt. Um diese nutzen zu können, musst du zuerst die Standardabweichung der Stichprobe kennen.
Standardfehler mit Mittelwert und Standardabweichung der Grundgesamtheit berechnen
Wenn Mittelwert und Standardabweichung der Grundgesamtheit gegeben sind, kommt folgende Formel zum Einsatz:
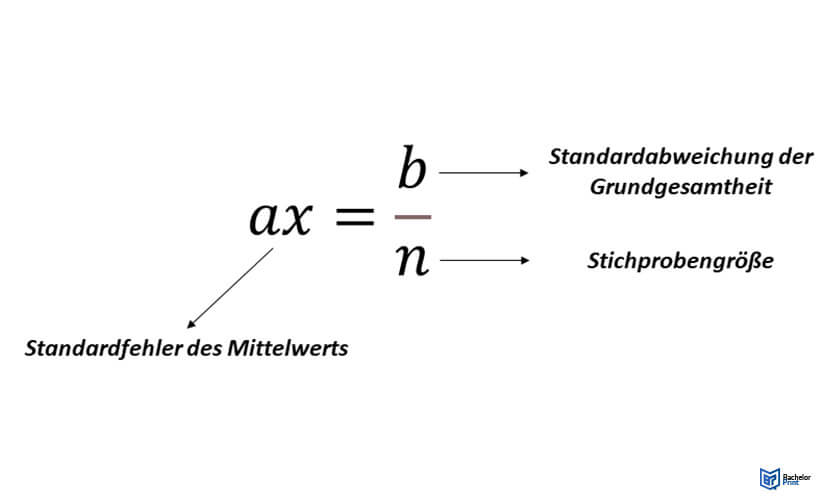
Es handelt sich stets um eine Schätzung des Standardfehlers, da du den Mittelwert der Stichprobe verwendet hast.
Standardfehler ohne Mittelwert und Standardabweichung der Grundgesamtheit schätzen
Sind dir Mittelwert und Standardabweichung der Grundgesamtheit unbekannt, wählst du folgende Formel:
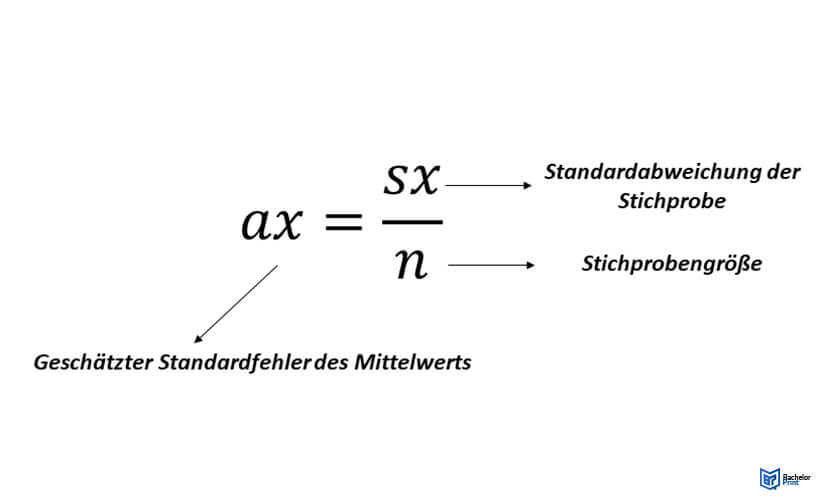
In wenigen Schritten zum Standardfehler des Mittelwerts
Es wäre zu aufwendig und auch unmöglich den Mittelwert der Grundgesamtheit ausfindig zu machen, wenn wir die Durchschnittsgröße von Frauen in Deutschland berechnen. Dies würde nämlich bedeuten, dass wir die Körpergröße jeder Frau in Deutschland messen müssten. Aus diesem Grund suchen wir nach einer praktischen Lösung. Es ist viel einfacher, eine Stichprobe zu ziehen und den Mittelwert der Stichprobe zu bestimmen. Anhand dessen können wir schließlich den Standardfehler schätzen.
Standardfehler und Standardabweichung im Vergleich
Sowohl der Standardfehler als auch die Standardabweichung sagen etwas über den Mittelwert einer Stichprobe aus. Der Standardfehler gibt Auskunft darüber, wie stark sich der Mittelwert der jeweiligen Stichprobe von demjenigen der Grundgesamtheit unterscheidet. Die Standardabweichung hingegen drückt aus, wie sehr die einzelnen Werte der Stichprobe von ihrem Mittelwert abweichen.
Wie berechnet man den Standardfehler in Excel?
Du kannst den Stichprobenfehler in Excel berechnen. Es gibt zwar keine direkte Formel, die du verwenden kannst. Daher musst du sie selbst eingeben.
Gib =STDEV(» «) /SQRT(count(» «)) ein. In den Klammern nennst du die Zellen der Werte, für die der Standardfehler bestimmt werden soll. Gib also die Zellen ein, damit Excel das Ergebnis errechnen kann. Auf diese Weise bekommst du das arithmetische Mittel sowie den Standardfehler angezeigt.
Häufig gestellte Fragen
Hier haben wir diejenigen Fragen zusammengefasst, die bei der Berechnung des Stichprobenfehlers am häufigsten gestellt werden.
Er gibt an, wie stark der Mittelwert einer Stichprobe vom Mittelwert der Grundgesamtheit abweicht. Dies ist insofern wichtig, weil immer nur eine Stichprobe erforscht werden kann.
Je größer die Stichprobe, desto geringer der Fehler. Einfacher ausgedrückt bedeutet dies, dass der Fehler kleiner ist, je mehr Personen oder Gegenstände befragt bzw. gemessen werden.
Es gibt zwei Möglichkeiten den Stichprobenfehler zu berechnen. Die Wahl der passenden mathematischen Formel hängt davon ab, ob die Standardabweichung der Grundgesamtheit gegeben ist. Ist die Standardabweichung der Grundgesamtheit unbekannt, kann man den Fehler lediglich schätzen.
Die Standardabweichung gibt die Streuung der Messwerte bezüglich des Mittelwerts an. Der Standardfehler hingegen drückt die Abweichung des Mittelwerts der Grundgesamtheit aus und stellt somit die Standardabweichung der Mittelwerte aller möglichen Stichproben dar, die man aus der Grundgesamtheit ziehen kann.
Die Berechnung dieses Wertes erfolgt in den unterschiedlichsten Bereichen. Sie kommt vor allem in der Statistik zum Einsatz.