
In diesem Beitrag erfährst du mehr über das Thema Korrelation in der Statistik. Zunächst lernst du die Definition. Danach erfährst du, wie sich Korrelationen bestimmen, interpretieren und berechnen lassen. Dabei gehen wir auf die Methoden zur Berechnung nach Pearson und Spearman ein. Zuletzt verraten wir dir mehr über das Streudiagramm als alternative Auswertung einer Korrelation sowie den kausalen Zusammenhang der Korrelation.
Definition: Korrelation
Der Begriff Korrelation stammt aus der Wissenschaft der Statistik. Der Ursprung des Wortes liegt in der lateinischen Sprache (von «correlatio») und bedeutet übersetzt Wechselbeziehung. Diese Beziehung betrifft zum Beispiel Funktionen, Merkmale oder Zustände. Man spricht hier allgemein auch von Variablen. Die Beziehung liegt also zwischen zwei oder mehreren Variablen vor.1
Es ist möglich, die Korrelation weiter zu unterteilen: Es gibt die Maßkorrelation bei intervallskalierten Merkmalen und die Rangkorrelation, die den linearen Zusammenhang zweier mindestens ordinal skalierter Variablen beschreibt. Darüber hinaus wird zwischen der positiven Korrelation und der negativen (oder inversen) Antikorrelation unterschieden, wenn es um die Richtung des Zusammenhangs geht.2
Bei positiven Korrelationen wächst oder schrumpft das eine Element, wenn auch das andere wächst oder schrumpft. Ein Beispiel: Wer mehr Überstunden macht, erhält auch mehr Lohn (zumindest theoretisch). Bei der Antikorrelation verhält es sich hingegen wie folgt: Wenn man mehr von einem Element hat, hat man weniger von dem anderen. Außerdem gibt es bei der Antikorrelation ebenfalls eine Umkehrung: Weniger von dem einen Element, mehr von dem anderen. Auch hier ein Beispiel: Wer mehr Überstunden macht, hat weniger Freizeit. Darüber hinaus können Variablen keinen Zusammenhang aufweisen.3
Korrelationen sind stets ungerichtet. Es geht also nicht darum, herauszufinden, welches Element das andere bedingt. Das bedeutet, dass die Beziehungen nicht kausal sind.4
Korrelation korrekt bestimmen und interpretieren
Mithilfe der Korrelation lässt sich mehr über den Zusammenhang der Variablen aussagen. Die Stärke des Zusammenhangs lässt sich konkret mit einer Maßzahl angeben, dem sogenannten Korrelationskoeffizienten.
Der Koeffizient wird mit dem Buchstaben r angegeben. Eine Einheit gibt es nicht. Der Korrelationskoeffizient kann im Bereich zwischen –1 und 1 liegen, wobei -1 und 1 jeweils für einen sehr starken und die 0 für keinen Zusammenhang stehen.5
| Korrelation | Variablenentwicklung | Beispiel |
| Positive Korrelation | Variable 1 steigt während Variable 2 steigt |
Wer viel einkauft, hat mehr Dinge. |
| Positive Korrelation | Variable 1 sinkt während Variable 2 sinkt |
Wer weniger einkauft, hat weniger Dinge. |
| Negative Korrelation | Variable 1 steigt während Variable 2 sinkt |
Wer mehr arbeitet, hat weniger Freizeit. |
| Negative Korrelation | Variable 1 sinkt während Variable 2 steigt |
Wer weniger arbeitet, hat mehr Freizeit. |
| Kein Zusammenhang | Variablen variieren nicht miteinander | Die Größe des Einkaufs hat nichts mit der Art der Arbeit zu tun. |
Die Korrelation berechnen – So geht’s
Um Korrelationen berechnen zu können, musst du zuerst den Korrelationskoeffizienten bestimmen. Hier spielt das Skalenniveau eine wichtige Rolle: Der Begriff bezeichnet Kategorien, die mehr über die Merkmale der Variablen verraten.
Darüber hinaus sind sie bei den Berechnungen der Korrelationskoeffizienten unumgänglich. Vier verschiedene Skalenniveaus sind von Bedeutung:
- Die Nominalskala
- Die Ordinalskala
- Die Intervallskala
- Die Ratioskala6
Berechnen einer Korrelation nach Pearson
Eine Methode zur Berechnung von Korrelationen hat der britische Mathematiker Karl Pearson geliefert. Sie ist die häufigste Methode zur Berechnung von Korrelationen und kommt zum Einsatz, wenn die Daten entweder metrisch oder dichotom sind. Ist das nicht der Fall, müssen andere Konzepte verwendet werden.
Als Kennzahl erhält man einen r-Wert zwischen -1 und 1. Der Korrelationskoeffizient wird in diesem Fall auch Pearson-Korrelation oder Bravais-Pearson-Korrelation genannt.7
Berechnen einer Korrelation nach Spearman
Der britische Psychologe Charles Edward Spearman hat ebenfalls eine Methode zur Berechnung von Korrelationen entwickelt. Dies führte zu einer Fehde mit Karl Pearson, der zur gleichen Zeit an derselben Universität arbeitete.8
Spearman prägte den Begriff des Spearman’schen Rangkorrelationskoeffizienten, der jedoch auch als Rangkorrelationskoeffizient nach Spearman bezeichnet wird. Für die Berechnung sind kontinuierliche Variablen erforderlich. Außerdem eignet sich die Methode nur, wenn die Daten ordinal skaliert sind.7
Das Streudiagramm als alternative Auswertung einer Korrelation
Bei Korrelationen ist es nicht unbedingt erforderlich, den Korrelationskoeffizienten zu ermitteln. Eine Alternative stellt das Erstellen eines Streudiagramms dar, das auch als Streuwolke oder Scatter Plot bekannt ist.
Bei diesem werden die Daten auf einem Koordinatensystem eingetragen. Eventuelle Zusammenhänge lassen sich auf den x- und y-Achsen besser sichtbar machen. Die x-Achse ist dabei für die Variable vorgesehen, die vermutlich die Ursache für die andere Variable ist. Letztere wird auf der y-Achse eingetragen.8
Streudiagramm Beispiel
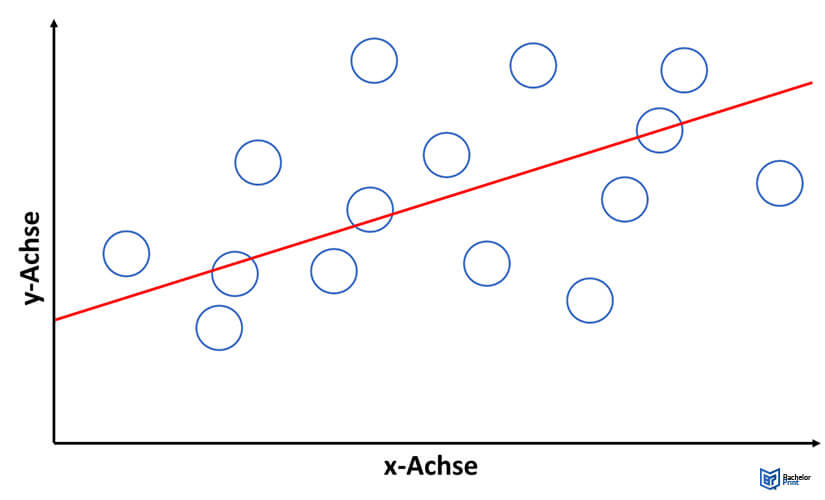
Erstellung eines Streudiagramms
Streudiagramme lassen sich auf verschiedenen Wegen erstellen, wenn sie gebraucht werden. Dazu kannst du unter anderem Tools wie SPSS, Excel oder Google Tabellen verwenden.
Bei YouTube und in zahlreichen Blogs findest du hochwertige Erklärungen, wie du mit diesen Tools Streudiagramme erstellen kannst.
Kausaler Zusammenhang einer Korrelation
Wenn du mit Korrelationen arbeitest, solltest du beachten, dass diese stets nur einen Hinweis auf eine Kausalität geben können. Sie sind keinesfalls ein Beweis. Dieser Fehler wird von Studenten häufig gemacht.
Möchtest du eine kausale Beziehung berechnen, solltest du stattdessen auf andere Methoden zurückgreifen. Geeignet sind zum Beispiel die Regressionsanalyse und die experimentelle Forschung.
Häufig gestellte Fragen
Bei Korrelationen handelt es sich um die Beziehung zwischen zwei oder mehr Variablen.
Dabei unterscheidet man unter anderem zwischen positiven und negativen Korrelationen. Es kann außerdem kein Zusammenhang zwischen den Variablen bestehen.
Um Korrelationen zu berechnen, stehen dir verschiedene Methoden zur Verfügung, zum Beispiel jene von Pearson und von Spearman.
Dadurch erhältst du einen Korrelationskoeffizienten, den du interpretieren kannst.
Die Werte des Korrelationskoeffizienten liegen im Bereich zwischen -1 und 1.
Der Koeffizient ist ein Wert, der zwischen -1 und 1 liegt. Er wird als r angegeben.
- Ist r größer als 1, liegt ein positiver Zusammenhang vor zwischen den Variablen der Korrelation.
- Ist r kleiner als 1, ist der Zusammenhang negativ.
- Bei r = 0 besteht kein linearer Zusammenhang.
Korrelationen sind nur ein Hinweis, nie aber ein Beweis für Kausalität.
Bei der Berechnung lässt sich nicht ermitteln, ob sich die Daten gemeinsam verändern. Als Beweis für Kausalität setzen Wissenschaftler auf andere Methoden wie die experimentelle Forschung.
Quellen
1 Prof. Dr. Kramps, Udo: Korrelation, in: Wirtschaftslexikon, 16.02.2018, [online] https://wirtschaftslexikon.gabler.de/definition/korrelation-40362 (14.12.2022)
2 Prof. Dr. Kramps, Udo: Maßkorrelation, in: Wirtschaftslexikion, 16.02.2018, [online] https://wirtschaftslexikon.gabler.de/definition/masskorrelation-37709 (14.12.2022)
3 Universität Zürich: Rangkorrelation nach Spearman, in: Methodenberatung, 23.02.2022, [online] https://www.methodenberatung.uzh.ch/de/datenanalyse_spss/zusammenhaenge/rangkorrelation.html (14.12.2022)
4 Universität Zürich: Korrelation nach Bravis-Pearson, in: Methodenberatung, 23.02.2022, [online] https://www.methodenberatung.uzh.ch/de/datenanalyse_spss/zusammenhaenge/korrelation.html (14.12.2022)
5 Uni Köln: Korrelationskoeffizient r, in: Uni Köln, o.D., [online] http://eswf.uni-koeln.de/glossar/node103.html (14.12.2022)
6 Universität Zürich: Skalenniveau, in: Methodenberatung, 23.02.2022, [online] https://www.methodenberatung.uzh.ch/de/Ressourcen–Beratung/skalenniveau.html (14.12.2022)
7 Gruber, Walter: Korrelation, in: WGruber, o.D., [online] https://wgruber.github.io/Modellbildung2/korrelationen.html (14.12.2022)
8 Welt der BWL: Streudiagramm, in: Welt der BWL, o.D., [online] https://welt-der-bwl.de/Streudiagramm (14.12.2022)
